Bitflip attack

AES-CBC - Theory

In CBC mode, AES uses 16-bytes blocks, we make sure that every message length is a multiple of 16 by using a padding standard such as PKCS7. ¹

In fact even when the message length is a perfect multiple of 16, a full padding block must be added, otherwise we’d have no way to distinguish between the end of the message and the beginning of the padding.

This is the academic representation of CBC encryption (regardless of the block cipher algorithm used)

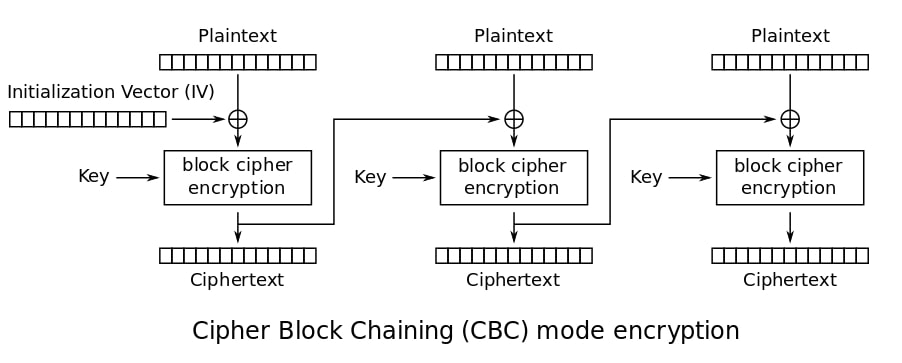
While the latter representation does a good job at picturing the general process, let us make it a little bit more specific for our use case :

In the following image, each square represents a 16 byte block. Each “phase” of the chaining only deals with the corresponding colored blocks. ( Disregard the uncolored squares to avoid confusion )

So, for instance, “phase” 1 processes the green block B₁ with IV to produce C₁ following the formula :

C₁ = E_k ( P₁ ^ IV )

The cipher result can be viewed as the concatenation of all sub ciphers C_i

Now, for the decryption part, things get more interesting …

The important aspect to understand here is that each block is decrypted using the previous cipher block.

In effect what happens after going through the decryption algorithm is :

P_i = C_i-1 ^ ( P_i ^ C_i-1 )

So if you happen to know P_i all what you have to do is to set C_i-1 like so :

C_i-1 = P_i ^ C_i-1 ^ X

Where X is the forged byte you want to replace the plain text with.

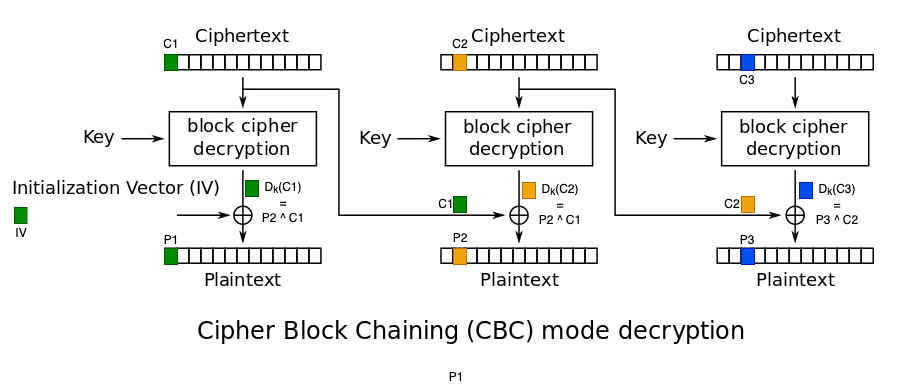
Now of course there are several things worth noticing before going to the demo :

• The modificiation of C_i-1 will corrupt P_i-1 (becomes gibberish)

• You must have the knowledge of the cipher to a known plaintext

• You can only modify the part of the plaintext you already know

Demo w/ Python

I got heavily inspired by a challenge i did recently and wanted to share the knowledge without blantly compromising the answer, so i refactored it to better suit this demo.

The script starts by initializing a random key and IV for the rest of the game.

1
2
3

from Crypto.Random import get_random_bytes
key = get_random_bytes(16)
iv = get_random_bytes(16)

Then, it asks you to enter a plaintext, and sends the corresponding cipher.

1
2
3
4
5
6
7
8
9
10
11
12
13

def encrypt_data(data):
	padded = pad(data.encode(),16,style='pkcs7')
	cipher = AES.new(key, AES.MODE_CBC,iv)
	enc = cipher.encrypt(padded)
	return enc.hex()
def main():
	msg = input("Your plaintext:")
	try:
		assert('y0ush4LIn0Tp45S' not in msg)
	except AssertionError:
		print('Not like this ...')
		raise
	print("Your ciphertext:" + encrypt_data(msg) + "\n")

Finally it asks you to enter a ciphertext.

1
2
3
4
5
6
7
8
9
10

	enc_msg = input("Enter ciphertext: ")
	
	try:
		check = decrypt_data(enc_msg)
		if check:
			print(" (ﾉ◕ヮ◕)ﾉ*:･ﾟ✧ Congratulations ! ٩(◕‿◕)۶")
		else:
			print(" ┐( ˘_˘ )┌ Try again ...  ᕕ( ᐛ )ᕗ")
	except Exception as e:
		print(e)

If it finds the pass phrase b’y0ush4LIn0Tp45S’ to be a substring of the decrypted ciphertext, you win !

1
2
3
4
5
6
7
8

def decrypt_data(data):
	cipher = AES.new(key, AES.MODE_CBC,iv)
	padded = cipher.decrypt( unhexlify(data))
	print(padded)
	if b'y0ush4LIn0Tp45S' in unpad(padded,16,style='pkcs7'):
		return 1
	else:
		return 0

In other words the goal of this challenge, is to craft a ciphertext that corresponds partly at least to the plain text : ‘y0ush4LIn0Tp45S’.

The entirety of the code can be found in my github : here

Let’s put in practice the theory !

Objective : Find an encrypted cipher that contains y0ush4LIn0Tp45S when deciphered.

As we obviously can not pass the phrase ‘y0ush4LIn0Tp45S’ (filtered by an assert clause), the idea is to get the ciphertext for most of the phrase except for one letter :

There are many ways to do this but i chose to replace the first letter with ‘a’ like so :

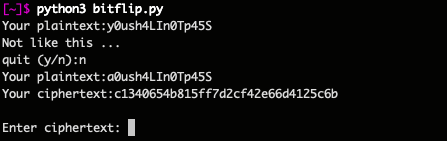
So this is the ciphertext of ‘a0ush4LIn0Tp45S’ given the random pair (key,iv):

1

c1340654b815ff7d2cf42e66d4125c6b

This is a hexstring, which means that 2 characters code for 1 byte, there is a total of 32 hex-characters in there equating to the block size of the AES-CBC encryption : 16 bytes.

The phrase we’ve entered ‘a0ush4LIn0Tp45S’ is 15 bytes long, so 1 padding byte will be appended to it, ( we can check the hexstring decoded by the algorithm right after entering the cipher and there is indeed the \x01 byte of padding as expected )

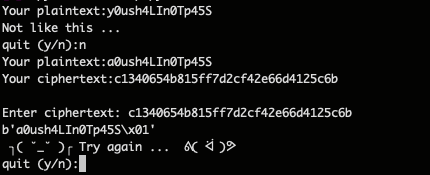
Now returning to our problem, how do we apply the bitflipping technique to this cipher in order to transform ‘a0ush4LIn0Tp45S’ to ‘y0ush4LIn0Tp45S’?

1

c1340654b815ff7d2cf42e66d4125c6b

One idea could be for instance to prepend the same hash right before it (no space):

1

c1340654b815ff7d2cf42e66d4125c6b c1340654b815ff7d2cf42e66d4125c6b

Then we’d apply the technique explained before to the first byte of the first cipher block, in order to transform the first byte of the second plaintext block:

C₁[0] ^ P₂[0] ^ ‘y’ = 0xc1 ^ ‘a’ ^ ‘y’ = 0xd9

So by replacing c1 to d9 in the first byte of the first cipher block we would get ?

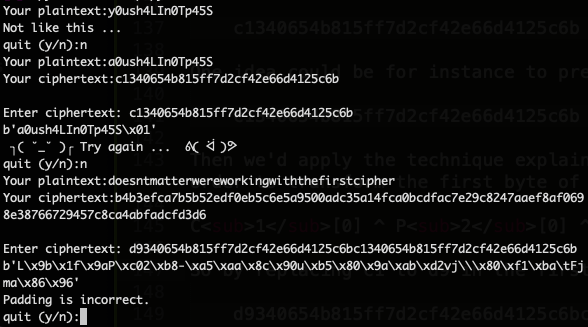
Oh no ! It doesn’t work, of course we expect the first block to be some gibberish (diffusion), but we’d expect the second block to be our passphrase. So what happened here ?

This is exactly why we need to remember that :

D_k(Ci) = C_i-1 ^ P_i

Essentially in our case :

D_k(C1) = IV ^ P₁

So what we were doing there was C₁[0] ^ P₂[0] ^ ‘y’ when what we really should be doing is rather IV₁[0] ^ P₂[0] ^ ‘y’ …

But wait a second, we don’t know what IV is, wasn’t the whole point of this attack to corrupt integrity without knowledge of the (key,iv) ?

Totally, and this is why, we need to offset our cipher target by one block, in such a way that it becomes :

D_k(C2) = C₁ ^ P₂

To achieve this, we just need to prepend our initial message phrase with a well crafted offset :

I chose for instance to duplicate our previous message (no space) :

1

a0ush4LIn0Tp45S a0ush4LIn0Tp45S

Now think about this for a second, if you keep things like that how will the blocks be formed (remember that the message was 15 bytes) :

1

a0ush4LIn0Tp45Sa 0ush4LIn0Tp45Sx01x01

So this is really what happens, now the problem is that we wanna change the second message letter ‘a’ to ‘y’ ² and to do that we use the corresponding block in the cipher.

But here the letter a of the second message is not in the beginning of the second block, so we can’t really affect it because it will be part of the gibberish output of D_k(C1).

To solve this minor issue, just realize that you have total control over the message’s body itself, so just by adding whatever random character there say ‘Z’ we get the following :

1

a0ush4LIn0Tp45SZ a0ush4LIn0Tp45Sx01

And voila, everything is in place for us to get some bitflippin’ :)

1

a0ush4LIn0Tp45SZa0ush4LIn0Tp45S

From our well-crafted phrase we get the cipher :

1

a0355ba433a8a1a8b15f1516ddf8ab97b54fd66aacf416b6a87dbde76837004e

Now our previous operation C₁[0] ^ P₂[0] ^ ‘y’ will definitely work, because this time indeed we have D_k(C2) = C₁ ^ P₂.

C₁[0] ^ P₂[0] ^ ‘y’ = 0xa0 ^ ‘a’ ^ ‘y’ = 0xb8

Here is a quick way to achieve that with python interactive :

And there we go we just need to flip the first byte ‘a0’ of the previously obtained cipher to ‘b8’ and feed that to the prompt :

1

b8355ba433a8a1a8b15f1516ddf8ab97b54fd66aacf416b6a87dbde76837004e